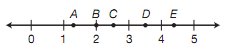
Which point on the number line represents the closest approximation to the square root of 12?
Explanation
Since \(3^{2}=9\) and \(4^{2}=16\), \(\sqrt{12}\)is between 3 and 4. Only point D lies between 3 and 4.
Visit our website for other GED topics now!
Related questions





