img-download-app
img-download-app

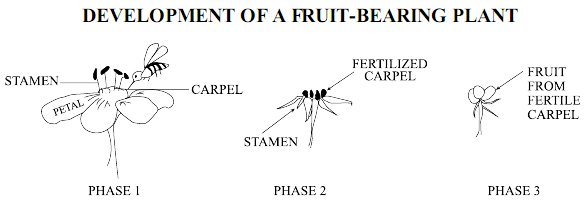
The Ionic Product of Water, \({K_{\rm{w}}}\) , is the equilibrium constant for the reaction in which water undergoes an acid-base reaction with itself.

\({K_{\rm{w}}} = \left[ {{H_3}{O^ + }_{(aq)}} \right]\left[ {O{H^ - }_{(aq)}} \right] = {10^{ - 14}}at25{}^oC\)

The value of \({K_{\rm{w}}}\) increases almost 75 times when temperature is increased from 0°C to 100°C .
If the \({K_{\rm{w}}}\) is  \(0.11 \times {10^{ - 14}}mo{l^2}d{m^{ - 6}}\) at 0°C . What would be the value of \({K_{\rm{w}}}\) at 100°C?

Explanation

As the value of \({K_{\rm{w}}}\) increases almost 75 times when temperature is increased from 0°C to 100°C. If value of \(K_{\mathrm{w}}\) is \(0.11 \times 10^{-14} \mathrm{~mol}^{2} d m^{-6}\) at 0°C, it would be \(0.11 \times 10^{-14} \times 75\)when temperature is increased 75 times i.e, at 100°C.
Supplement: \(0.11 \times \$75 \sim \$ 8.25\)

Visit our website for other GED topics now!
Related questions
Phase 1: The flower attracts insects, which pollinate the carpel, resulting in fertilization. After fertilization occurs, the flower’s petals wither.
Phase 2: A seed develops inside each carpel, an ovary wall encases each seed, and the ovary swells to form a pericap, while the flower’s stamens wither.
Phase 3: The seed and pericap form a fruit, which attracts animals.

Among the following, which is probably responsible for spreading fruit-bearing plants from one location to another?
The more reactive a metal to oxygen, the more it tends to corrode. The table would be useful in the production of any of the following EXCEPT which one?
Pathogens in the form of airborne droplets are most likely to cause which of the following illnesses?
The border between two air masses is referred to as a front. An advancing front can be either warm or cold. What happens along a cold front?z
A food pyramid is shown below. In this food pyramid, toads are which of the following?
Which of the following is NOT one of the ways in which the carbon cycle uses carbon to build organic compounds?
The Smiths have four children, all girls. Their fifth child is a boy. Why did this change occur?
The visible light spectrum contains varying wavelengths, each appearing as a distinct color. White light contains the entire color spectrum. Objects around us exhibit their particular colors because they reflect the wavelengths of only those colors while absorbing all other wavelengths. Why is a ripe banana yellow in color?
Air is composed of nitrogen, oxygen, argon, carbon dioxide, and other gasses. How may air be best described?
In 1969, two scientists devised an experiment to test a hypothesis that the number of species in an ecosystem depends on the area of the ecosystem. They counted all the arthropod species on a few very tiny islands. They then exterminated all the arthropods (mostly insects) with a pesticide. Over six months, they monitored the gradual repopulation of the island and noticed that by the end of the observation period, each island had almost the same number of species as it had before pesticide was used. However, the kinds of species that arrived often differed from the species that were on the island prior to pesticide use. Here is a chart that illustrates the results.
Based on the chart, which trophic level suffered the greatest net loss (number of species) in diversity?
Which of the following statements is correct in comparing and contrasting prokaryotes and eukaryotes?
All of the following may inhibit enzymatic reactions EXCEPT
What are the principles of conduction?
All of the following are steps of photosynthesis EXCEPT
A telescope’s large aperture (opening) enables it to collect more light than the human eye can. This feature is important to detect dim, distant stars as well as to distinguish a star’s features, some of which appear lighter than others. Increasing a telescope’s magnification by shortening the focal length of a lens makes a small, blurry image appear as a larger, blurry image.

What is the best way to detect specific features of a distant star?

A particle at rest will stay at rest and a particle in motion will stay in motion until acted upon by an outside force.
Fundamentally, the human body is composed of billions of tiny cells. These cells are, in turn, composed of various components working in perfect harmony, called organelles. The nucleus is one such organelle. Which of the following is one function that the nucleus performs, apart from its role as the chief coordinator of all the cell’s activities?
Evaporation happens when high-energy molecules in a liquid escape from the liquid’s surface and get converted into vapours. As particles with greater energy keep on leaving the liquid as time goes on, the liquid’s temperature keeps on dropping as well. Which of the following properties of the liquid do you think will lead to an increase in the rate of evaporation? 
Which statement about energy and/or matter is incorrect?
Ionization Energy (I.E.) is the amount of energy needed to force an electron out of an atom. The ‘${1^{st}}$ Ionization Energy’ is the amount of energy needed to expel the first electron out of an atom’s outermost shell. The ‘${2^{nd}}$ Ionization Energy’ is the energy required to expel the second electron from the atom and so on. 
Which of the following variables can have any sort of effect on the value of ionization energy for an element or a compound?
Osmosis is the movement of water across a selectively permeable membrane in order to equalize the concentration (the amount of protein per milliliter of water) on two sides of the membrane. Consider the diagram below. The container is divided into two compartments, A and B, by a selectively permeable membrane. Each circle represents 100 protein molecules that can't pass through the membrane. The amount of water on two sides of the membrane is initially equal.What will happen as a result of osmosis?
One similarity between animal and bacterial cells is that both contain ribosomes. What is another similarity between the two?
Artificial cardiac pacemakers are implanted in a defective heart to take care of which cardiac function?
If heat is added to a liquid which of the following occurs?
A and B are travelling with the same velocity. If Object A is to have greater momentum than Object B, which of the following would have to be true?
What is the main difference between a glucose molecule and a fructose molecule?
Isomers are molecules that have the same number of the same elements, but in a different arrangement.Which one of the following is an isomer of 2-propanol (shown below), which contains Carbon (C), Hydrogen (H) and Oxygen (O)?